Ferroresonance is usually associated with potential transformers, which are instrument transformers that are used to develop voltages used by relays; however, it can also occur with power transformers under special circumstances.
Ferroresonance is another occurrence that can cause equipment damage; fortunately, it is preventable by simply avoiding certain types of transformer connections with the types of circumstances that enable it to occur.
Because these connections are routinely avoided in practice, ferroresonance is not encountered very often and there isn’t much information about it in the literature.
Ferroresonance is worthy of mention, however, because it can utterly destroy a transformer.
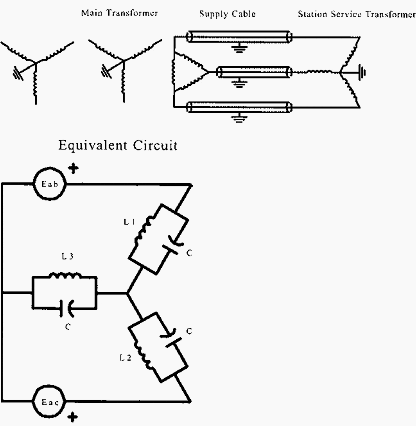
Figure 1 - A situation where ferroresonance may occur. The cable capacitances form three parallel L-C elements that are in series with each other and the source voltages.
The necessary conditions for ferroresonance are established in the system shown in Figure 1.
In the example shown in Figure 1, the ∆-connected tertiary winding of a large three-winding substation transformer supplies a distribution type station-service transformer with a Grd.-Y primary winding. The supply lines to the station-service transformers are through a set of shielded cables. If the cable runs are fairly long, a significant amount of phase-to-ground capacitance may exist.
When a transformer core operates near saturation, the B-H curve is highly nonlinear, and the effective permeability of the core can take on a range of values that vary with the changes in flux density.
Each of the inductances shown as L1, L2, and L3, will have instantaneous inductance values that are proportional to the effective permeability of the core at any given instant in time. These inductances form parallel L-C circuits that are in series with one another and in series with the source voltage.
Since L1, L2, and L3 are constantly varying along with the effective permeability of the core, it is almost certain that a series resonant condition will exist at least part of the time during every cycle.
When a series resonance exists, even for a brief period, this causes very large voltages across the L-C elements.
These voltages are capable of destroying the transformer and any other equipment connected to it.
The nonlinear nature of this problem makes mathematical analysis virtually impossible, but the phenomenon has been observed both in the field and experimentally, and the voltages have been measured and recorded.
In the example above, the conditions for ferroresonance can be disrupted by the simple expedient of ∆-connected secondary winding to the station service transformer.
The ∆-connected winding assures that the vector sum of the voltages of all three phases add to zero, stabilizing the neutral point of the Y-connected primary winding and preventing excessive voltage across the windings. The presence of a ∆-connected secondary winding will essentially ‘‘snuff out’’ ferroresonance in this circuit.
No comments:
Post a Comment